此篇文章為我在研究利用車載IMU判斷行進方向並預防事故的一些技術資料整理及個人理解。 可能在學術上不是很嚴謹,也有可能有地方有錯誤。 名詞定義上也可能和其他學術論文不同。
環境
*** IMU(Inertial measurement unit): 慣性測量單元 *** IMU包含加速度計、磁力計、陀螺儀等sensor 而IMU被包進後照鏡中,掛在車子上 目的是希望車子行進時,可以計算出車子的方向或是其他資訊來幫助後續處理
座標系
所謂座標系,像我們高中數學、物理所學的直角座標系、慣性座標系也是座標系的一種 而這裡我們主要討論的是「地球座標系」
*** 地球座標系(Earth Frame) *** 這裡的地球座標系,指的是x軸指向北方,y軸指向東方,z軸指向地心的座標系 所以在地球座標系上,重力加速度平行z軸,且垂直xy平面 (xy平面即為水平面)
*** 載體座標系(Body Frame) *** 載體座標系在這裡指的是,相對於車子的座標系 例如:車子行進方向為x軸,左右方向為y軸,垂直兩者的為z軸 而在車上的物體就能以此座標系來表示 一般都將Sensor Frame簡化成Body Frame
歐拉角
歐拉角分為三種角度:roll、pitch、yaw
*** roll *** roll一般指的是繞x軸旋轉的角度 就是往x軸看過去,yz平面上旋轉的角度
*** pitch *** pitch一般指的是繞y軸旋轉的角度
*** yaw *** yaw一般指的是繞z軸旋轉的角度
對於一個三維剛體的旋轉來說,roll、pitch、yaw三個角度可以定義出該剛體的旋轉情形
以我們的環境來說,後照鏡(IMU)因為每次掛在車上時的角度都不同,所以我們用"目前後照鏡的座標系" 與 “地球座標系"之間的角度差異來定義我們IMU傾斜的幅度 而兩個座標系的角度差異即可用roll、pitch、yaw來表示
例如:水平擺放的IMU轉了roll角,再轉了pitch,最後轉yaw角,變成目前掛在後照鏡上的狀態(傾斜角度) 這個我們稱為傾角補償
而這裡旋轉的先後是有差別的,先旋轉roll或先旋轉pitch,最後的結果有可能不同 所以可能有不同組(roll, pitch, yaw)旋轉可以對應到同一個物體的傾斜狀態
方位角
又稱為Azimuth
這裏的方位角定義為車子在水平面上的行進方向與磁北在水平面上的投影的夾角
此方位角即可拿來作為車子行進方向(heading)的依據
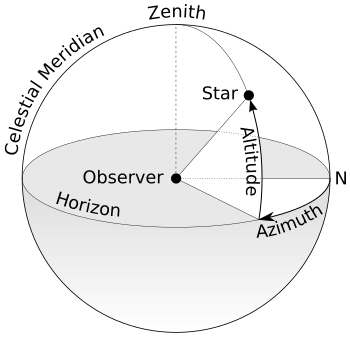
仔細觀察即可發現,Azimuth其實就是yaw角(相對於水平面來說)
若IMU為水平擺放,且磁力計x軸為車行進方向,則Azimuth的值即為arctan(my/mx)
(mx: 磁力計x軸測得之數值 ; my: 磁力計y軸測得之數值)
計算方位角、歐拉角
由於IMU擺放通常不會是水平的,所以我們必須計算出IMU的roll、pitch角度 來去修正磁力計的資料,並計算出Azimuth (這邊磁力計還會受到外界磁場干擾,如軟硬磁干擾等,需要先校正) 一般利用加速度計+磁力計得到Azimuth的步驟是這樣: 1. 由加速度計去計算roll跟pitch 2. 透過剛剛計算的roll跟pitch將磁力計座標系修正至地球座標系 3. 修正完之後,計算磁力向量在水平面上跟車頭方向的夾角,即為所求
關於第一點的解釋:
因為車子靜止時只會受到向下的重力加速度,正常來說水平擺放時其中一個軸是平行重力加速度
所以當IMU不是水平擺放時可以用加速度分量算出旋轉的角度
但是並不是所有歐拉角都能單靠加速度計算出來
舉例來說:
水平擺放時,Z軸與重力加速度平行,但今天面向北方和面向東方,加速度計測到的讀數都相同
此時繞著Z軸旋轉的姿態角(yaw),就無法單靠加速度計得到。
除了磁力計和加速度計可以計算出歐拉角之外 也可以利用陀螺儀得到歐拉角,方法如下: 1. 陀螺儀的讀數為角速度 2. 對時間做積分即為角位移(角度變化) 3. 若有初始姿態,則理論上可以透過角位移推出所有歐拉角 但是由於是積分的關係,雜訊、誤差會不斷累積,隨時間被放大
但兩種方法各有優缺,像加速度計在快速震動(高頻)時,容易有誤差干擾。 而陀螺儀在幾乎靜止(低頻)的狀態容易有漂移(drift)的問題。 解決這種狀況的方法之一就是下面要介紹的互補濾波器:
互補濾波器(Complementary Filter)
所謂的濾波器,就是能幫我們過濾掉不需要資訊的玩意。 濾波器有分很多種,像平均濾波器、卡爾曼濾波器等等 互補濾波器是將高頻的陀螺儀算出的角度,跟低頻的加速度計算出的角度,依照比例相加 藉而得到誤差影響程度較低的角度
公式: Angle = Gyro_Angle * a + (1 - a) * Acc_Angle,Gyro_Angle為陀螺儀算出的角度; Acc_Angle為加速度計算出的角度
其中 0 < a < 1
其他
*** atan2 ***
C/C++當中的atan2(y, x),是我們這個研究當中會很常用到的函數
它的意義是求y/x的反正切值
返回值介於[-pi/2, pi/2]
具體一點來說就是以x軸轉到(x,y)向量的角度
若y>0: 所得之值為x軸逆時針計算的角度
若y<0: 所得之值為x軸順時針計算的角度
舉例:
1. atan2(-1, 1) * 180 / PI == -45度
2. atan2(1, -1) * 180 / PI == 135度
[剩下的較詳細資料有空的話再補上。這部分研究耗了我不少腦力,如果有錯還請指正]